Theorie der Wahl der Verbraucher unter Risiko in der Volkswirtschaft
Theorie der Wahl der Verbraucher unter Risiko in der Wirtschaft!
Inhalt:
1. Die Bernoulli-Hypothese
2. Das Neumann-Morgenstern-Messverfahren
3. Die Friedman-Savage-Hypothese
4. Die Markowitz-Hypothese
5. Kritische Bewertung der modernen Nutzenanalyse
Die moderne Nutzenanalyse ist das Ergebnis des Versagens der Indifferenzkurvenmethode, das Konsumentenverhalten unter riskanten oder unsicheren Entscheidungen zu erklären. Die traditionelle Nutzenanalyse befasst sich auch mit dem Verbraucherverhalten bei risikolosen Entscheidungen. Solche Entscheidungen sind sicher, da sie auf dem Prinzip der Verringerung des Grenznutzens und auf der Verhältnismäßigkeitsregel beruhen.
Der Verbraucher ist sich seines Einkommens, seines Geschmacks und der von ihm gekauften Waren sicher und maximiert seine Zufriedenheit, indem er die Kombination wählt, die ihm den höchsten Gesamtnutzen bietet. In der Realität sind jedoch viele Waren und Dienstleistungen mit Risiken oder Unsicherheiten behaftet, beispielsweise in Aktien, Versicherungen und Glücksspiel.
Es waren Neumann und Morgenstem, die in ihrer Theorie der Spiele und des wirtschaftlichen Verhaltens das Verhalten eines Individuums in riskanten Situationen untersuchten. Ihre Theorie wurde von Friedman und Savage und von Markowitz verfeinert. Die Lösung des Problems riskanter Situationen wurde von Daniel Bernoulli bereitgestellt, der versuchte, das Petersburger Paradoxon zu lösen. Wir erläutern diese unterschiedlichen Ansichten zu Entscheidungen, die Risiken oder Unsicherheiten beinhalten.
Die Bernoulli-Hypothese:
Die neoklassische Theorie geht davon aus, dass der Konsument ein vernünftiges Wesen ist, das sich nicht mit Glücksspielen oder auch nur mit fairen Wetten und einer Quote von 50-50 vergnügt. Der Grund, warum die Leute nicht bereit waren, auch bei fairen Wetten zu wetten, wurde von Daniel Bernoulli, dem Schweizer Mathematiker aus dem 18. Jahrhundert, zur Verfügung gestellt.
Bernoulli hielt sich 1732 für einige Zeit in St. Petersburg auf und stellte fest, dass die Russen nicht bereit waren, Wetten mit einer Quote von mehr als 50-50 zu tätigen. Sie wussten völlig, dass ihre mathematischen Erwartungen, Geld in einer bestimmten Art von Glücksspiel zu gewinnen, umso größer waren, je mehr Geld sie wetten . Dieser Widerspruch ist als St. Petersburger Paradox bekannt. Um es zu erklären, hat Bernoulli das folgende Spiel komponiert.
Eine Münze wird geworfen und eine Zahlung wird an den Spieler geleistet, abhängig davon, welcher Wurf des Unternehmens zuerst "Köpfe" erscheint. Wenn beim ersten Wurf Köpfe auftreten, erhält der Spieler 2 € und das Spiel wird gestoppt. Kommt es im zweiten Wurf, wird £ 2 2 = £ 4 bezahlt und das Spiel wird gestoppt. Wenn Köpfe zum ersten Mal nach n Würfen angezeigt werden, werden dem Spieler £ 2 n ausgezahlt. Wie viel wäre eine vernünftige Person bereit, für die Teilnahme an diesem Spiel zu zahlen? Oder wie hoch ist der erwartete Geldwert der Auszahlung für ein solches Spiel? Der erwartete Geldwert des Spiels ist unendlich. Die Wahrscheinlichkeit, dass der Kopf beim ersten Münzwurf auftritt, beträgt 1/2. Die Wahrscheinlichkeit, Köpfe zum ersten Mal beim n-ten Wurf zu erhalten, beträgt (1/2) n . Da es keine endliche Anzahl von Würfen gibt, bei denen garantiert werden kann, dass ein Kopfball auftritt, die erwartete Auszahlung des Spiels oder der erwartete Geldwert des Spiels,
EMV = ( 1/2 ) 2 + ( 1/2 ) 2 2 2 + ( 1/2 ) 3 2 3 + ………… .. + ( 1/2 ) n.2n
cc
= Σ ∞ n = 1 ( 1/2 ) n 2 n = 1 + 1 + 1 +…. + 1…
= unendlich
Da der EMV unendlich ist, wäre eine Person, deren Ziel es ist, den erwarteten Geldwert zu maximieren, bereit, alles zu zahlen, was er zum Spielen des Spiels braucht. Bernoulli entschied das St. Petersburger Paradoxon, indem er vorschlug, dass die Leute nicht bereit wären, ihr gesamtes Einkommen für ein solches Spiel zu zahlen, dass der Grenznutzen des Geldes mit steigendem Einkommen sinkt.
Eine Person, die Rs setzt. 100 zu gleichen Gewinn- oder Verlustquoten. 10 spielt das Spiel nicht, wenn er ein vernünftiges Wesen ist. Wenn er gewinnt, hat er Rs. 110, die gleich dem Nutzen des Nutzens von Rs sind. 10 gewonnen zu Rs. 100. Wenn er verliert, hat er Rs. 90, was gleich dem Verlust des Nutzens von Rs ist. 10 verloren von Rs abgezogen. 100.
Obwohl der monetäre Gewinn oder Verlust gleich ist, ist der Verlust an Nutzen größer als der Gewinn an Nutzen in diesem Spiel. Nach Ansicht von Bernoulli würden vernünftige Entscheidungen bei riskanten Entscheidungen auf der Grundlage der Erwartungen des Gesamtnutzens und nicht der mathematischen Erwartungen des Geldwerts getroffen. Dies ist in Abbildung 1 dargestellt.

Wobei TU die Gesamtnutzungskurve ist, die bei höheren Einkommensniveaus immer steiler wird, was auf einen abnehmenden Grenznutzen des Einkommens hinweist. Angenommen, die Person befindet sich auf dem Einkommensniveau OY (in unserem Beispiel 100 Rs), wodurch sie sich als OU eignet. Er überlegt, ob er eine faire Wette annehmen soll oder nicht, mit einer Wahrscheinlichkeit von 50-50, entweder sein Einkommen auf OY 2 (Rs. 110) zu erhöhen oder auf OY 1 (Rs. 90) um den gleichen Betrag zu reduzieren.
Er wird die Auswirkungen auf seinen Nutzen prüfen. Wenn sein Einkommen auf OY 2 steigt, steigt sein Nutzen auf OU 2, und wenn sein Einkommen auf OY 1 sinkt, fällt sein Nutzen auf OU 1 . Wie aus der Abbildung hervorgeht, ist der Nutzenverlust von UU 1 größer als der Nutzengewinn von UU 2. Der Verlust oder Gewinn des Gesamtnutzens bezieht sich auf den Grenznutzen. Da die Erwartung eines Nutzungsausfalls größer ist als der Nutzwert, akzeptiert diese Person keine faire Wette.
Bernoullis Lösung für das St. Petersburger Paradoxon hinsichtlich des erwarteten Nutzens anstelle des erwarteten Geldwerts des Spiels veranlasste Neumann und Morgenstem, ihren Nutzenindex unter riskanten Entscheidungen aufzubauen.
Das Neumann-Morgenstern-Messverfahren
J. Von Neumann und O. Morgenstem entwickelten in ihrem Buch Theory of Games and Economic Behavior die Methode der Kardinalmessung des erwarteten Nutzens aus riskanten Entscheidungen, die bei Glücksspielen, Lotterielosen usw. zu finden sind wird als NM-Hilfsindex bezeichnet.
Annahmen:
Der NM-Versorgungsindex basiert auf den folgenden Annahmen:
(1) Die Person verhält sich in riskanten Situationen, um den erwarteten Nutzen zu maximieren.
(2) Seine Entscheidungen sind transitiv: Wenn er einen Preis (Gewinn) dem Preis und einen C vorgezogen hat, zieht er A bis C vor.
(3) Es gibt eine Wahrscheinlichkeit P, die zwischen 0 und 1 liegt (0 <P <1), so dass das Individuum zwischen dem sicheren Preis A und den Lottospielen, die mit der Wahrscheinlichkeit P und mit der Wahrscheinlichkeit P bzw. 1 - P Preise anbieten, gleichgültig ist.
(4) Wenn zwei Lotterielose die gleichen Preise anbieten, zieht die Person das Lotterielos mit der höheren Gewinnwahrscheinlichkeit vor.
(5) Das Individuum kann Wahrscheinlichkeitskombinationen unbestimmter Entscheidungen vollständig anordnen.
(6) Die Ungewissheit oder das Risiko besitzt keinen eigenen Nutzen oder Nicht-Nutzen.
Der NM Utility Index:
Neumann und Morgenstern haben die folgende Methode zur Messung des Nutzenindex vorgeschlagen. „Betrachten Sie drei Ereignisse, С, A, B, für die die Reihenfolge der individuellen Präferenzen die festgelegte ist. Sei a eine reelle Zahl zwischen 0 und 1, so dass A genau gleich wünschenswert ist, wenn das kombinierte Ereignis aus einer Änderung der Wahrscheinlichkeit 1 für a und der verbleibenden Wahrscheinlichkeit der Wahrscheinlichkeit a für C besteht. Dann schlagen wir die Verwendung von a vor als numerische Schätzung für das Verhältnis der Präferenz von A gegenüber В zu der von С gegenüber B. "
Ihre Formel wird zu A = B (1- a + aC). Ersetzen Sie P durch eine Wahrscheinlichkeit, haben wir A = (1-P) + PC
Unter den Annahmen ist es möglich, einen Kardinalwertindex auf der Grundlage der obigen Formel abzuleiten.
Angenommen, es gibt die drei Ereignisse (Lotterien) С, A, B. Von diesen Ereignissen (Lotterie) A ist sicher, С hat Wahrscheinlichkeit P und ¨ Wahrscheinlichkeit (1-P), und wenn ihre jeweiligen Dienstprogramme U a sind, U b und U c dann U a = PU c (1-P) U b
Da erwartet wird, dass der Verbraucher den Nutzen maximiert, muss der Nutzen von A mit Sicherheit gleich einem Wert P sein, dem erwarteten Nutzen der Ereignisse (Lotterien) С und.
Um einen Utility-Index basierend auf der NM-Gleichung zu erstellen, müssen Sie die Utility-Werte С und B zuweisen. Diese Utility-Werte sind willkürlich, mit der Ausnahme, dass einem bevorzugten Ereignis (Lotterie) ein höherer Wert zugewiesen werden sollte. Angenommen, wir weisen die folgenden willkürlichen Gebrauchswerte zu: U c = 100 utils, U b = 0 util und P = 4/5 oder 0, 8
U a = (4/5) 100 + (1-4 / 5) (0)
= 80 + (1/5) (0) = 80
Somit ist der Nutzenindex in dieser Situation
Situation U a U b U c
1 80 0 100
Auf diese Weise kann man Gebrauchswerte für U a, U b, U c usw. ableiten und einen vollständigen NM-Nutzindex für alle möglichen Kombinationen erstellen, wobei von zwei beliebigen Situationen ausgegangen wird, die Risikowahrscheinlichkeiten beinhalten.
Es ist eine Bewertung:
Der NM-Hilfsindex bietet eine konzeptionelle Messung des Kardinalnutzens unter riskanten Entscheidungen. Es soll dazu verwendet werden, Vorhersagen über zwei oder mehr Alternativen in Bezug auf Glücksspiele, Lottoscheine usw. zu treffen und aus diesen eine, die eine Person bevorzugen kann.
Der NM-Index basiert auf den erwarteten Werten der Dienstprogramme. Es bietet eine Methode, um den Grenznutzen von Geld hauptsächlich zu messen. Es bezieht sich jedoch nicht darauf, ob der Grenznutzen des Geldes abnimmt oder zunimmt. In diesem Sinne ist diese Methode der Nützlichkeitsmessung unvollständig.
Das NM-Kardinal-Utility unterscheidet sich jedoch vom neoklassischen Cardinal-Werkzeug. Es ist nicht wie Längen- oder Gewichtsmaße. Sie misst auch nicht die Intensität der introspektiven Zufriedenheit oder des Vergnügens von Waren und Dienstleistungen, wie dies beim neoklassischen Nutzen der Fall ist. “ Die NM-Methode zur Messung des Nutzens analysiert die Handlungen einer Person, die riskante Entscheidungen trifft.
Trotz der Tatsache, dass der NM-Nutzenindex willkürlich ist, ist er bis zu einer linearen Transformation messbar. Es beinhaltet nicht additiv, sondern erlaubt die ordinale Messung relativer Präferenzen bei riskanten Entscheidungen.
Die Friedman-Savage-Hypothese:
Die Neumann-Morgenstern-Methode basiert auf den erwarteten Werten der Versorgungsunternehmen und bezieht sich daher nicht darauf, ob der Grenznutzen des Geldes abnimmt oder zunimmt. In dieser Hinsicht ist diese Methode der Nützlichkeitsmessung unvollständig. Wenn eine Person eine Versicherung erhält, zahlt sie für die Flucht oder die Vermeidung von Risiken. Wenn er jedoch ein Lottoschein kauft, hat er eine kleine Chance auf einen großen Gewinn.
Somit geht er ein Risiko ein. Manche Menschen kaufen sowohl Versicherungen als auch Glücksspiele und vermeiden und entscheiden sich daher für Risiken. Warum'? Die Antwort wurde von der Freedman-Savage-Hypothese als Erweiterung der NM-Methode geliefert.
Es besagt, dass der Grenznutzen von Geld für Einkommen unter einem bestimmten Niveau abnimmt, dass es für Einkommen zwischen diesem Niveau und einem höheren Einkommensniveau ansteigt und wieder bei allen Einkommen über diesem höheren Niveau sinkt. Dies ist in Fig. 2 in Bezug auf die Gesamtnutzungskurve TU dargestellt, wobei der Nutzen auf der vertikalen Achse und der Ertrag auf der horizontalen Achse aufgetragen sind.
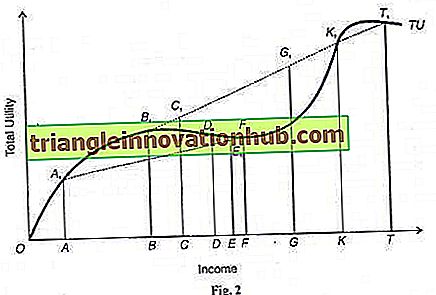
Angenommen, eine Person kauft für ihr Haus eine Versicherung gegen die geringe Chance eines schweren Feuerschadens und auch ein Lottoschein, das eine kleine Chance auf einen großen Gewinn bietet. Ein solches widersprüchliches Verhalten einer Person, die eine Versicherung kauft und auch Glücksspiele abschließt, wurde von Friedman und Savage mit einer Gesamtnutzungskurve gezeigt. Eine solche Kurve steigt zunächst mit abnehmender Geschwindigkeit, so dass der Grenznutzen des Geldes abnimmt, und steigt dann mit zunehmender Geschwindigkeit an, sodass der Grenznutzen des Einkommens steigt.
Die Kurve TU in der Figur steigt zuerst bis zum Punkt F 1 nach unten und dann bis zum Punkt K 1 nach oben. Angenommen, das Einkommen der Person aus ihrem Haus ist OF mit FF 1, ohne Feuer. Jetzt kauft er eine Versicherung, um das Risiko eines Feuers zu vermeiden. Wenn das Haus durch Feuer niedergebrannt wird, wird sein Einkommen mit AA-Nutzen auf OA reduziert. Durch das Zusammenfügen der Punkte A 1 und F 1 erhalten wir Nutzpunkte zwischen diesen beiden unsicheren Einkommenssituationen. Wenn die Wahrscheinlichkeit eines Feuers P ist, dann ist das erwartete Einkommen dieser Person auf der Grundlage des NM-Versorgungsindex
Y = P (OF) + (1-P) (OA).
Wenn das erwartete Einkommen (Y) der Person OE ist, dann ist ihr Nutzen EE 1 auf der gestrichelten Linie A t F r. Nehmen wir nun an, dass die Versicherungskosten (Versicherungsprämie) FD sind. Das versicherte Einkommen der Person mit Versicherung ist daher OD (= OF-FD), was ihm einen höheren Nutzen DD 1 als EE 1 aus dem erwarteten Einkommen OE mit Wahrscheinlichkeit eines Brandes verleiht. Daher wird die Person eine Versicherung abschließen, um Risiken zu vermeiden, und das gesicherte Einkommen OD erhalten, indem sie eine FD-Prämie entrichtet, falls sein Haus durch Feuer niedergebrannt wird.
Da die OD-Einnahmen der Person nach dem Abschluss einer Feuerschutzversicherung des Hauses verbleiben, beschließt er, ein Lotterielos zu kaufen, das die DB kostet. Wenn er nicht gewinnt, fällt sein Einkommen mit dem Versorger BB 1 auf OB. Wenn er gewinnt, würde sich sein Einkommen mit dem Nutzen KK 1 auf OK erhöhen. Somit ist sein erwartetes Einkommen mit der Wahrscheinlichkeit P ', dass es keine Lotterie gibt
Y 1 = P '(OB) + (1 -P') (OK)
Wenn das erwartete Einkommen F der Person ОС ist, dann ist dessen Nutzen CC 1 auf der gestrichelten Linie B 1 K 1, was ihm einen größeren Nutzen (CC 1 ) verleiht, indem er das Lottoschein kauft, als DD 1, wenn er es nicht gekauft hätte. So wird die Person auch das Ticket zusammen mit einer Versicherung für das Haus gegen Feuer kaufen.
Nehmen wir das erwartete Einkommen der OG im steigenden Teil F 1 K 1 der TU-Kurve, wenn der Grenznutzen des Einkommens steigt. In diesem Fall ist der Nutzen des Lottoscheins GG 1, der größer als DD 1 ist, wenn er die Lotterie nicht kaufen würde. So wird er sein Geld für die Lotterie einsetzen.
In der letzten Phase, in der das erwartete Einkommen der Person in der Region K 1 T 1 der TU-Kurve mehr als OK ist, nimmt der Grenznutzen des Einkommens ab und er ist daher nicht bereit, Risiken beim Kauf von Lottoscheinen oder im Internet einzugehen andere riskante Anlagen mit Ausnahme günstiger Quoten. Diese Region erklärt St. Petersburg Paradox.
Friedman und Savage glauben, dass die TU-Kurve die Einstellung der Menschen zu Risiken in verschiedenen sozioökonomischen Gruppen beschreibt. Sie erkennen jedoch viele Unterschiede zwischen Personen auch in derselben sozioökonomischen Gruppe. Einige sind gewöhnliche Spieler, während andere Risiken vermeiden. Dennoch glauben Friedman und Savage, dass die Kurve die Neigungen der Hauptgruppen beschreibt.
Ihrer Meinung nach sind Personen in der mittleren Einkommensgruppe mit zunehmendem Einkommensnutzen diejenigen, die bereit sind, Risiken einzugehen, um ihr Los zu verbessern. Wenn es ihnen gelingt, mit Risiken mehr Geld zu verdienen, heben sie sich in die nächsthöhere sozioökonomische Gruppe auf. Sie wollen nicht nur mehr Konsumgüter. Sie wollen vielmehr in der sozialen Dimension aufsteigen und ihre Lebensgewohnheiten ändern. Deshalb steigt der Grenznutzen des Einkommens für sie.
Die Markowitz-Hypothese:
Prof. Markowitz fand die Friedman-Savage-Hypothese entgegen den üblichen Beobachtungen. Seiner Meinung nach ist es nicht richtig zu sagen, dass die Armen und die Reichen nicht bereit sind zu spielen und Risiken einzugehen, außer wenn dies günstig ist. Vielmehr kaufen sowohl Lotterien als auch Glücksspiele bei Pferderennen. Sie spielen auch in Casinos und spielen an der Börse.
So haben Friedman und Savage das tatsächliche Verhalten der Armen und Reichen nicht beachtet, weil sie davon ausgehen, dass der marginale Nutzen des Einkommens vom absoluten Einkommensniveau abhängt. Markowitz hat es geändert, indem es den Grenznutzen des Einkommens mit den Änderungen des gegenwärtigen Einkommens in Beziehung setzt.
Nach Markowitz führt ein Anstieg des Einkommens um einen kleinen Zuwachs zu einer Erhöhung des Grenznutzens des Einkommens. Starke Einkommenssteigerungen führen jedoch zu einer Verringerung des geringfügigen Einkommensnutzens. Aus diesem Grund zögern Menschen bei höheren Einkommen, sich auch bei fairen Wetten dem Glücksspiel zu widmen, und Personen, die in langsam steigenden Einkommensgruppen leben, gönnen sich dem Glücksspiel, um ihre Position zu verbessern.
Auf der anderen Seite steigt bei geringfügigen Einkommensrückgängen der Grenznutzen des Einkommens. Ein starker Einkommensrückgang führt jedoch zu einer Verringerung des geringfügigen Einkommensnutzens. Aus diesem Grund versichern die Menschen gegen kleine Verluste, gönnen sich jedoch Glücksspielen, bei denen große Verluste entstehen.
Dies wird als Markowitz-Hypothese bezeichnet, die in Abbildung 3 erläutert wird. Markowitz nimmt im oberen Teil des Diagramms drei Wendepunkte M, N und P mit aktuellem Einkommen im mittleren Punkt N der TU-Einkommenskurve an.
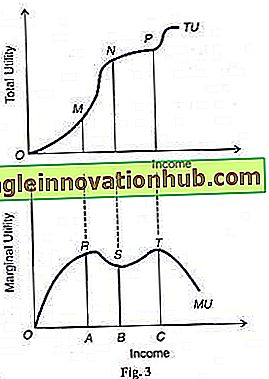
Der Grenznutzen der Einkommenskurve MU wird im unteren Teil des Diagramms abgeleitet, wo das aktuelle Einkommensniveau OB ist. Bei einem geringfügigen Anstieg des Einkommens einer Person von OB auf ОС steigt der Grenznutzen des Einkommens von Punkt S bis T der MU-Kurve. Starke Einkommenssteigerungen über ОС hinaus führen jedoch zu einem abnehmenden Grenznutzen der Erträge ab Punkt T entlang der MU-Kurve.
Auf der anderen Seite führen geringfügige Einkommensrückgänge von OB zu О A zu einer Erhöhung des Grenznutzens von Einkommen von S zu R auf der MU-Kurve. Ein starker Einkommensabfall links von A führt jedoch zu einer Verringerung des Grenznutzens von Einkommen von Punkt R zu О entlang der MU-Kurve.
Die Markowitz-Hypothese ist eine Verbesserung gegenüber der Friedman-Savage-Hypothese. Anstelle des absoluten Einkommensniveaus wird das derzeitige Einkommensniveau einer Person verwendet. Es legt nahe, dass das Verhalten einer Person gegenüber Versicherungen und Glücksspielen dasselbe ist, unabhängig davon, ob sie arm oder reich ist. Der Schwerpunkt liegt auf kleinen oder großen Erhöhungen oder Abnahmen des gegenwärtigen Einkommens einer Person, die sein Verhalten gegenüber Versicherungen und Glücksspielen bestimmt.
Kritische Bewertung der modernen Nutzenanalyse:
In der modernen Nutzenanalyse des Risikos oder der Ungewissheit impliziert die Neumann- und Morgenstem-Hypothese einen messbaren Nutzen bis hin zu einer linearen Transformation, wodurch der marginalen Nutzen wieder verringert oder erhöht wird. Die Friedman-Savage-Hypothese enthält ein zusätzliches Element.
Es wird versucht, die Form der Kurve des Gesamtnutzungsnutzens zu erklären. Diese Hypothesen sind somit Versuche, die Nützlichkeitsmessung zu rekonstruieren. Die NM-Theorie der riskanten Entscheidungen zusammen mit ihren Varianten wie der Friedman-Savage-Hypothese und der Markowitz-Hypothese war jedoch in zwei Punkten immer noch Gegenstand von Kontroversen. erstens aus praktischer Sicht und zweitens, ob es sich um eine Kardinal- oder eine Ordinalmethode handelt.
Zum einen ist es fraglich, ob das Risiko messbar ist, wenn Neumann und Morgenstem davon ausgehen, dass das Risiko keinen eigenen Nutzen oder keine Unzulänglichkeit besitzt, sie ignorieren die Freuden oder Schmerzen der Unsicherheit.
Zweitens ist das Element der Unsicherheit in der Mehrzahl der individuellen Entscheidungen sehr gering.
Drittens sind individuelle Entscheidungen unendlich groß. Garantiert, dass sie unsicher sind, ist es möglich, sie mit der NM-Methode zu messen. Schließlich misst es nicht die "Gefühlsstärke" des Einzelnen gegenüber Gütern und Dienstleistungen unter unsicheren Entscheidungen.
Die Frage, ob die NM-Methode den Nutzen hauptsächlich oder ordinal misst, ist unter den Ökonomen sehr verwirrend. Robertson verwendet es in seinem Utility und All That im kardinalen Sinn, während Profs. Baumol, Fellner und andere sind der Ansicht, dass die Rangfolge des Nutzens ordinal ist. Die NM-Theorie hat nach Baumol nichts mit der neoklassischen Theorie über die Kardinalität zu tun.
In der neoklassischen Theorie wird der Begriff "Kardinal" verwendet, um die introspektive absolute Grenzwertmessung des Nutzens zu bezeichnen, während er in dieser Theorie operativ verwendet wird. In der NM-Theorie werden den Lotteriescheinen gemäß der Rangfolge der Preise einer Person die Nutzennummern zugewiesen, und die Vorhersage wird numerisch getroffen, welche der beiden Tickets ausgewählt wird. Obwohl die NM-Formel verwendet wird, um den Nutzenindex abzuleiten, sagt sie nichts über die Verringerung des Grenznutzens aus. Somit ist das NM-Utility nicht das neoklassische Kardinal-Utility.
Die Verfeinerungen von Friedman-Savage und Markowitz haben dazu geführt, dass die neoklassische Annahme, dass der marginale Nutzen des Einkommens für alle Einkommensbereiche abnimmt, aufgegeben wird. Somit ist die Theorie der Nützlichkeitsmessung bei riskanten Entscheidungen dem neoklassischen introspektiven Kardinalismus bestimmter Entscheidungen überlegen.
Ökonomen wie Dorfman, Samuelson und Solow haben die paretianischen Nützlichkeitsindizes von der NM-Formel abgeleitet. Und wenn der NM-Index basierend auf dem individuellen Ranking erstellt wird, vermittelt er Informationen über seine Präferenzen.
Die NM-Messung verwendet Baumol im ordinalen Sinne weiter, wenn er den NM-Grenznutzen mit der Grenzsubstitutionsrate gleichsetzt. Er schreibt: „Der NM-Grenznutzen X endet als höchstens die Substitutionsrate zwischen und die Wahrscheinlichkeit des Gewinns des vorgegebenen Preises (E) des Standard-Lottos. Dies ist sicherlich keine Kardinalmessung im klassischen Sinne. “